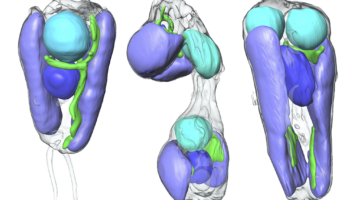
In two recent papers, an international team of scientists describe the first known nitrogen-fixing organelle within a eukaryotic cell. The organelle is the fourth example in history of primary endosymbiosis—the process by which a prokaryotic cell is engulfed by a eukaryotic cell and evolves beyond symbiosis into an organelle. Read more »
All News & Updates
Shedding Light on Sea Creatures’ Secrets
Exactly how does coral make its skeleton, a sea urchin grow a spine, or an abalone form the mother-of-pearl in its shell? A new study at the ALS revealed that this process of biomineralization, which sea creatures use to lock carbon away in their bodies, is more complex and diverse than previously thought. Read more »
Suggest Speakers and Workshops for the 2024 User Meeting
The 2024 ALS User Meeting will take place August 12–14. Help shape this year’s program by submitting nominations for plenary speakers and proposing workshops and tutorials by April 4. Read more »
Winter 2024 Shutdown Recap
The ALS is back in user operation after more than two months of shutdown. Major achievements include the mechanical installation for the new booster bend power supplies and the two power supplies for the accumulator ring radio frequency system. Read more »
Room-Temperature 2D Magnet: Electronic-Structure Insights
Researchers found that small changes in how electron spins interact with each other can make a big difference in the magnetic transition temperatures of 2D magnets. Understanding such factors can help create better magnetic materials for information storage, sensors, medical imaging, and energy-efficient computing. Read more »![]()
![]()
Monika Choudhary, Computing Postdoc
As a postdoc, Monika Choudhary applies computing models to real experimental data at the ALS, work that uses her extensive computer science knowledge and experience. Read more about the path that led her to the ALS and the people she’s met along the way. Read more »
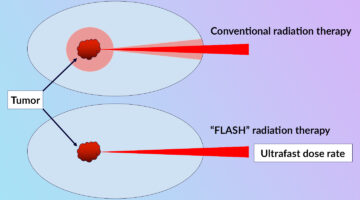
Clarifying the FLASH Effect for Cancer Radiation Therapy
To clarify the underlying mechanisms of the FLASH effect, in which the delivery of ultrafast, high-intensity doses of radiation to tumors counterintuitively reduces damage to surrounding healthy cells, researchers directly compared the oxidative effects of conventional and FLASH techniques using x-ray footprinting at the ALS. Read more »
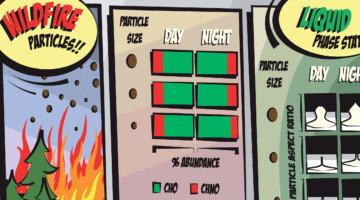
Case Study of Aerosol Particles Influenced by Wildfire
Researchers studied atmospheric aerosols influenced by wildfires in the Pacific Northwest. They examined the connection between particle size, chemical composition, and phase state, in particles collected during the day and at night. The information is important for modeling the effects of wildfire smoke on atmospheric properties. Read more »
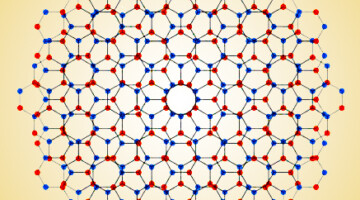
Big Twist Leads to Tunable Energy Gaps in a Bilayer Stack
Researchers found that twisting 2D layers at atypically large angles opens up potentially useful energy gaps in the material’s band structure. The results suggest a new way to tune materials for optoelectronic applications and provides a platform for exploring novel “moiré” phenomena beyond those observed at small twist angles. Read more »![]()
![]()
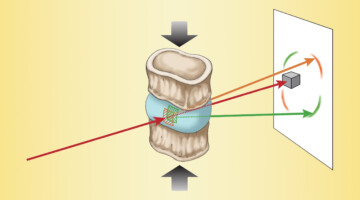
The Effects of Diabetes on Spinal-Column Biomechanics
Researchers found that type 2 diabetes induces earlier onset of plastic (nonrecoverable) deformation in intervertebral discs by impairing the biomechanical behavior of collagen. A greater understanding of the underlying causes of tissue failure in diabetes—a growing problem worldwide—is important in helping to prevent and treat symptoms. Read more »![]()
- 1
- 2
- 3
- …
- 123
- Next Page »